
The equilateral triangle is a well-known Deity symbol that has been used by nearly every religion since Ancient Egyptian times. Wherever you look, you will see the number three reflected in nature, making triangles the ultimate symbols of completeness. Other popular meanings of the three triangle points include the mind, body, and spirit, as well as the past, present, and future. Similar versions can be found in Hinduism and Paganism to represent the Divine in its threefold nature. The Christian holy trinity, which represents the Father, Son, and Holy Spirit, is perhaps the most well-known of these. The three points of a triangle are also significant but their meanings differ slightly between religions. Therefore, they symbolize the stages of growth that ultimately lead to enlightenment. Triangles are wide at the base and taper to a point at the tip. If any symbol(s) in this list resonates with you, you can use it in your life to help you in your own spiritual journey. In this article let’s look at 28 spiritual triangle symbols and their meaning and their significance to cultures around the world. L.The triangle has been used as a symbol of spiritualism and enlightenment since the dawn of human civilization. (This explains the naming convention.) It follows that every obtuse triangle is self-conjugate with respect to its polar circle. A triangle with this property is called self-conjugate with respect to the circle. The same fact affords a reformulation: the sides of the triangle are the polars of the opposite vertices with respect to the polar circle. Since inversion maps circles onto circle, the circumcircle of ABC is inverted into the circumcircle of H aH bH c. The proof is immediate from (2): the inversion in the polar circle exchanges vertices of a triangle with the feet of the altitudes, so that, for example, A is mapped on H a. The applet helps grasp the following fact: the circumcircle and the 9-point circle of an obtuse triangle are inverse images of each other in the polar circle of the triangle. In the second pair of circles (drawn in magenta), one is the 9-point circle of ΔABC (the circumcircle of ΔH aH bH c) the second one is its inverse image in the green circle. (Note that the two red circles cross on the green one.) When the radius of the latter is such that the two red circles coincide, you can observe that the circles are orthogonal.
One of the red circles is the circumcircle of ΔABC the second one is its inverse image in the green circle. The radius of the latter is controlled by the scrollbar at the bottom of the applet. There is also a green circle centered at the orthocenter.
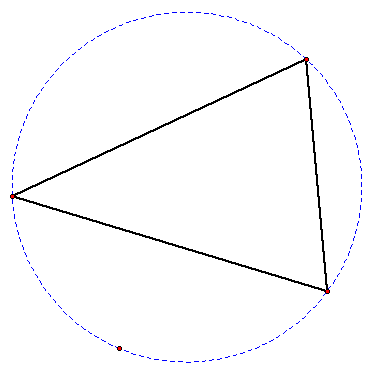
The applet shows a triangle with the altitudes and four (two red and two magenta) circles drawn. The polar circle is only defined for obtuse triangles. Thus the polar circle of ΔABC is centered at the orthocenter and have the radius R defined by (2)

This circle is known as the polar circle of ΔABC. The endpoints of those tangents lie on a circle centered at H and perpendicular to all three circles. (1) then means that the tangents from H to the three circles are equal. If the feet of the altitudes opposite the vertices A, B, C are denoted H a, H b, H c, then the powers of the point H with respect to the three circles are equal: (1)įor an obtuse triangle, the orthocenter lies outside the triangle and outside each of the three circles. The orthocenter H of ΔABC serves as the radical center of the circles constructed on the sides of the triangle as diameters. |Activities| |Contact| |Front page| |Contents| |Geometry| Copyright © 1996-2018 Alexander Bogomolny
#Triangle with circle outside install
If you want to see the applet work, visit Sun's website at, download and install Java VM and enjoy the applet. This applet requires Sun's Java VM 2 which your browser may perceive as a popup.


 0 kommentar(er)
0 kommentar(er)
